 Liczby i wyrażenie - Liczby całkowite i działania na nich - Liczby naturalne Liczby i wyrażenie - Liczby całkowite i działania na nich - Liczby naturalne
Liczbami naturalnymi nazywamy liczby: 0,1,2,3,4,...
Tak więc liczba uczniów w klasie jest liczbą naturalną, natomiast temperatura powietrza może, ale nie musi wyrażać się liczbą naturalną.
W zbiorze liczb naturalnych istnieje liczba najmniejsza, jest nią liczba 0. Nie ma w tym zbiorze jednak liczby największej, bo jeśli n jest liczbą naturalną, to n+1 też jest liczbą naturalną.
Zbiór liczb naturalnych oznacza się przez N,
N = {0,1,2,...}.
Na liczbach naturalnych można wykonywać dodawanie i mnożenie.
Wynik dodawania liczb a, b nazywamy sumą a+b, natomiast liczby, które dodajemy, składnikami.
Wynik mnożenia liczb a, b nazywamy iloczynem a x b, natomiast liczby, które mnożymy, czynnikami.
Wynik odejmowania liczb a, b nazywamy różnicą a—b, natomiast liczbę a nazywamy odjemną, a liczbę b odjemnikiem.
Wynik dzielenia liczb a, b nazywamy ilorazem a : b, natomiast liczbę a nazywamy dzielną, a liczbę b dzielnikiem.
Wynik dodawania, a także wynik mnożenia liczb naturalnych jest zawsze liczbą naturalną i dlatego mówimy, że działania te są wykonalne w zbiorze liczb naturalnych. Inaczej jest z odejmowaniem i dzieleniem liczb naturalnych. Różnica dwu liczb naturalnych może być liczbą naturalną (np. 7—3 = 4), ale może też być liczbą ujemną (np. 4—9 = —5). Podobnie jest z ilorazem liczb naturalnych, gdyż iloraz liczb naturalnych może być liczbą naturalną (np. 6:2 = 3), ale może nie być liczbą naturalną
np. 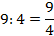 . Dlatego mówimy, że odejmowanie i dzielenie nie są działaniami wykonalnymi w zbiorze liczb naturalnych. . Dlatego mówimy, że odejmowanie i dzielenie nie są działaniami wykonalnymi w zbiorze liczb naturalnych.

Liczby i wyrażenie - Liczby całkowite i działania na nich - Pisemne wykonywanie działań na liczbach naturalnych
Przy pisemnym dodawaniu i odejmowaniu bardzo istotne jest właściwe podpisywanie liczb, to znaczy podpisuje się pod sobą cyfry jedności, cyfry dziesiątek, cyfry setek itd.
Przykład
Najpierw dodajemy jedności (9 + 5 = 14). Podpisujemy pod jednościami 4 i 1 dziesiątkę dodajemy do dziesiątek (1+8+4= 13). Znowu podpisujemy 3 pod dziesiątkami i 1 setkę dodajemy do setek (1+7 + 6= 14). Pod setkami podpisujemy 4 i 1 tysiąc dodajemy do tysięcy (1+4 = 5).
Przykład
Najpierw odejmujemy jedności. Ponieważ 1—3 nie jest wykonalne w zakresie liczb naturalnych, więc zwiększamy liczbę jedności o 10 (1 dziesiątkę) i mamy 11—3 = 8. Następnie odejmujemy dziesiątki, pamiętając o tym, że jedną dziesiątkę wykorzystaliśmy przy odejmowaniu jedności. Należy więc od 3 dziesiątek odjąć 5 dziesiątek. Tutaj też nie ma dosyć dziesiątek, wobec tego zwiększamy ich liczbę i mamy 13 — 5 = 8 itd.
Przypominamy teraz zasadę mnożenia pisemnego.
Przykład
| |
|
|
2 |
3 |
5 |
4 |
| x |
|
|
1 |
4 |
6 |
3 |
| |
|
|
7 |
0 |
6 |
2 |
| |
1 |
4 |
1 |
2 |
4 |
|
| |
9 |
4 |
1 |
6 |
|
|
| 2 |
3 |
5 |
4 |
|
|
|
| 3 |
4 |
4 |
3 |
9 |
0 |
2 |
2354 X 1463 = 2354 (1000+400+60 + 3).
Najpierw mnożymy 2354 X 3 (jedności) i zaczynamy podpisywać iloczyn 7062 pod jednościami. Następnie mnożymy 2354 X 6 (dziesiątek) i zaczynamy podpisywać iloczyn 14124 pod dziesiątkami. W dalszym ciągu mnożymy 2354 X 4 (setki) i zaczynamy podpisywać iloczyn 9416 pod setkami. Wreszcie 2354 X 1 (tysiąc) i zaczynamy podpisywać iloczyn pod tysiącami. Przy mnożeniu bardzo ważne jest właściwe podpisywanie iloczynów cząstkowych. Na koniec otrzymane iloczyny cząstkowe dodajemy.
Pisemny sposób dzielenia wyjaśnimy na przykładzie.
Przykład
| |
|
|
5 |
5 |
2 |
|
|
|
| |
1 |
5 |
4 |
6 |
8 |
: |
2 |
8 |
| - |
1 |
4 |
0 |
|
|
|
|
|
| |
|
1 |
4 |
6 |
|
|
|
|
| |
- |
1 |
4 |
0 |
|
|
|
|
| |
|
|
|
6 |
8 |
|
|
|
| |
|
|
- |
5 |
6 |
|
|
|
| |
|
|
|
1 |
2 |
|
|
|
Dzielenie zaczynamy od liczb utworzonych z cyfr występujących z lewej strony w zapisie dzielnej. Ponieważ 28 nie mieści się w 15, więc musimy podzielić 154 przez 28. Liczba 28 mieści się w 154 pięć razy. Ten iloraz cząstkowy (5) zapisujemy nad cyfrą setek dzielnej (4). Następnie mnożymy 28 X 5, otrzymany iloczyn 140 podpisujemy pod 154 i wykonujemy odejmowanie (154-140 = 14). Do różnicy 14 dopisujemy następną cyfrę dzielnej (6) i otrzymujemy 146. Dalej postępujemy jak wyżej. Otrzymany wynik oznacza, że 15468 = 28 X 552+12, co można inaczej zapisać
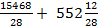

Liczby i wyrażenie - Liczby całkowite i działania na nich - Liczby całkowite
Liczbami całkowitymi nazywamy liczby naturalne oraz liczby do nich przeciwne, to znaczy 0; 1 i - 1; 2 i - 2; 3 i - 3 itd.
W zbiorze liczb całkowitych nie ma liczby największej ani liczby najmniejszej. Zbiór liczb całkowitych oznacza się przez C, C = {...-3, -2, -1, 0, 1, 2, 3...}.
Dodawanie i mnożenie w zbiorze liczb całkowitych ma takie same własności jak w zbiorze liczb naturalnych.
W zbiorze liczb całkowitych są wykonalne: dodawanie, mnożenie i odejmowanie. (Odejmowanie, jak zauważyliśmy poprzednio, nie jest wykonalne w zbiorze liczb naturalnych.)

Liczby i wyrażenie - Liczby całkowite i działania na nich - Wartość bezwzględna liczby
Określenie. Wartością bezwzględną liczby nieujemnej jest ta liczba. Wartością bezwzględną liczby ujemnej jest liczba do niej przeciwna. Zapisujemy to wzorem:
| |
|
|
|
|
a, |
|
gdy |
|
a |
|
|
|
0 |
|
|
| |a| |
= |
{ |
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
- |
a, |
|
gdy |
|
a |
|
< |
|
0 |
|
|
Określenie to wyjaśnimy na przykładach.
Przykłady
|5| = 5, |3| = 3,
|0| =0
|-7| = 7, |-100| = 100
Warto zwrócić uwagę na fakt, że liczba a może być liczbą dodatnią lub ujemną lub 0. Jeśli a > 0 (a jest liczbą dodatnią), to - a < 0 ( — a jest liczbą ujemną). Natomiast jeśli a < 0 (a jest liczbą ujemną), to —a > 0 ( -a jest liczbą dodatnią). Wnioskujemy stąd, że wartość bezwzględna liczby różnej od 0 jest zawsze liczbą dodatnią.

Liczby i wyrażenie - Liczby całkowite i działania na nich - Dodawanie liczb całkowitych
Aby dodać dwie liczby o jednakowych znakach, dodajemy ich wartości bezwzględne. Suma jest liczbą takiego znaku, jak każda z dodawanych liczb.
Przykłady
( + 5)+(+12) = +17,
(-7)+(-18) = -25.
Aby dodać dwie liczby o różnych znakach, od większej wartości bezwzględnej odejmujemy mniejszą. Wynik jest liczbą takiego znaku, jaki ma liczba o większej wartości bezwzględnej.
Przykłady
(-5)+( + 12) = +7,
(-15)+( + 8) = -7.
Dla 0 obowiązuje zasada a + 0 = a.

Liczby i wyrażenie - Liczby całkowite i działania na nich - Odejmowanie liczb całkowitych
Aby od jednej liczby odjąć drugą, należy do pierwszej z tych liczb dodać liczbę przeciwną do drugiej liczby, a—b = a+ (—b).
Przykłady
(-7)-(+3) - (-7)+(-3) = -10,
( + 8)-( + 5) = ( + 8)+ (-5) = +3 = 3,
(-18)-(-10) = (—18)+ (+10) = -8,
(+14)-(-4) = (+14)+(+4) = +18 = 18.

Liczby i wyrażenie - Liczby całkowite i działania na nich - Mnożenie liczb całkowitych
Aby pomnożyć dwie liczby o jednakowych znakach, mnożymy ich wartości bezwzględne. Iloczyn jest liczbą dodatnią.
Przykłady
( + 4) x (+6) = +24 = 24,
( -8) x ( -3) = +24 - 24.
Aby pomnożyć dwie liczby o różnych znakach, mnożymy ich wartości bezwzględne. Iloczyn jest liczbą ujemną.
Przykłady
(-12) x (+3) = -36,
(+ 5) x (-8) = - 40.
Dla mnożenia przez 0 obowiązuje zasada a x 0 = 0.

Liczby i wyrażenie - Liczby całkowite i działania na nich - Dzielenie liczb całkowitych
Aby podzielić dwie liczby o jednakowych znakach, dzielimy ich wartości bezwzględne. Iloraz jest liczbą dodatnią.
Przykłady
(-18) : (-2) = +9 = 9,
( + 27) : ( + 3) = +9 = 9.
Aby podzielić dwie liczby o różnych znakach, dzielimy ich wartości bezwzględne. Iloraz jest liczbą ujemną.
Przykłady
(-36) : ( + 6) = -6,
(+42) : (-7) = -6.
Jeżeli dzielną jest 0, to obowiązuje zasada 0 : a = 0 (dla a ≠ 0). Jeżeli dzielnikiem jest 0, to dzielenie nie jest wykonalne. Należy pamiętać, że nie wolno dzielić przez zero.
Powyższe zasady można wytłumaczyć następująco. Wiadomo, że 15:3 = 5, bo 3 x 5 = 15. Podobnie 0 : 5 = 0, bo 0 x 5 = 0.
Zastanówmy się obecnie, co otrzymalibyśmy dzieląc np. 5 : 0. Jeśli przyjmiemy, że 5 : 0 = a, to a x 0 = 5, ale jak wiadomo a x 0 zawsze równa się 0, nie może więc równać się 5. Stąd dzielenie przez 0 nie jest możliwe.
GRUPA MEDIA INFORMACYJNE & ADAM NAWARA |