Pozostałe hobby Jeśli chcesz poznać ciekawych ludzi, ciekawe miejsca, dać się porwać ekscytującym wrażen11iom, poczuć przyspieszone tętno, mocniejsze bicie serca, skosztować wolności, odkryć swoje hobby, pasje to możesz to uczynić razem z Nami – Pasjonatami Grupy Media Informacyjne.

Hipoteza wytężeniowa (1904)

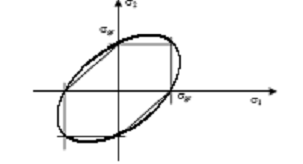
rys. 7.  Obszar dopuszczalny w płaskim stanie naprężenia wg hipotezy Hubera

Maksymilian Tytus Huber był wyjątkową postacią w dziejach polskich nauk ścisłych i technicznych. Jego pionierskie, odkrywcze prace badawcze na wielu polach mechaniki teoretycznej i stosowanej uszeregowały go w rzędzie najwybitniejszych uczonych naszej epoki. Dorobek Hubera stanowi istotny w skali światowej wkład do rozwoju tej dziedziny wiedzy.

W trakcie nauki w szkole politechnicznej we Lwowie, pracował naukowo. Opublikował swe prace: "Prosta konstrukcja hiperboli" oraz "Nowy wykreślny sposób wyznaczania momentów bezwładności figur płaskich" we lwowskim "Czasopiśmie technicznym". Stopniowo jego zainteresowania matematyczne skupiły się na tych zagadnieniach, które mają znęcenie dla zastosowań technicznych.
Od 1899 roku wykładał mechanikę teoretyczną i budowlaną na Wyższej Szkole Przemysłowej w Krakowie. W 1904 roku uzyskał stopień doktora nauk technicznych za pracę "Przyczynek do teorii stykania się ciał sprężystych", stanowiącą istotny wkład w teorię sprężystości. rozwiązał w niej obliczeniowo zagadnienie tzw. bezwzględnej miary twardości. W tym samym roku opublikował w " Czasopiśmie Technicznym" najważniejszą ze swych prac: "Właściwa praca odkształcenia jako miara wytężenia materiału". Sformułował w niej hipotezę: "można z wielkim prawdopodobieństwem uważać energię odkształcenia postaciowego za miarę wytężenia materiału". Jest to tak zwany warunek plastyczności stanowiący podstawowe kryterium klasycznej teorii plastyczności. Hipoteza ta doczekała się uznania dopiero w ćwierć wieku później. Wysunęli ją von Mises i H. Hencky, ale priorytet Hubera na ogół nie jest kwestionowany.

Wytężenie materiału jest w wytrzymałości materiałów stanem materiału obciążonego siłami zewnętrznymi, w którym istnieje niebezpieczeństwo przejścia w stan plastyczny (przekroczenie granicy sprężystości, jeśli materiał taką posiada lub utrata spójności, czyli pękniecie, przełom, dekohezja).

Wytężenie materiału określa się przez redukcję złożonego stanu naprężenia do jednego naprężenia zredukowanego lub zastępczego. To naprężenie może być porównane z podstawowymi wytrzymałościowymi stałymi materiałowymi: wytrzymałością na rozciąganie Rm lub naprężeniem rozrywającym Ru, które uzyskuje się w czasie statycznej próby rozciągania. Do redukcji złożonego stanu naprężenia stosuje się hipotezy wytężeniowe. Najczęściej stosowana jest właśnie hipoteza energii odkształcenia sformułowana przez Maksymiliana T. Hubera, która zakłada, że ciało jest doskonale sprężyste, i że praca naprężenia zredukowanego równa jest sumie prac wszystkich naprężeń składowych. Hipoteza wytężeniowa zastosowana do podstawowych stanów obciążenia pozwala na przeprowadzanie odpowiednich obliczeń wytrzymałościowych.

GRUPA MEDIA INFORMACYJNE & ADAM NAWARA

Jeśli chcesz poznać ciekawych ludzi, ciekawe miejsca, dać się porwać ekscytującym wrażen11iom, poczuć przyspieszone tętno, mocniejsze bicie serca, skosztować wolności, odkryć swoje hobby, pasje to możesz to uczynić razem z Nami – Pasjonatami Grupy Media Informacyjne.

Jeśli chcesz poznać ciekawych ludzi, ciekawe miejsca, dać się porwać ekscytującym wrażen11iom, poczuć przyspieszone tętno, mocniejsze bicie serca, skosztować wolności, odkryć swoje hobby, pasje to możesz to uczynić razem z Nami – Pasjonatami Grupy Media Informacyjne.

Jeśli chcesz poznać ciekawych ludzi, ciekawe miejsca, dać się porwać ekscytującym wrażen11iom, poczuć przyspieszone tętno, mocniejsze bicie serca, skosztować wolności, odkryć swoje hobby, pasje to możesz to uczynić razem z Nami – Pasjonatami Grupy Media Informacyjne.