Czas -zadania
Zadanie 1.
Która godzina czasu słonecznego miejscowego jest w Krakowie (20°E), jeżeli w Madrasie (81°E) jest godzina 1600 tego czasu?
Rozwiązanie:
Obliczamy różnicę długości geograficznej między Madrasem a Krakowem:
81°E - 20°E = 61°
Obliczamy różnicę czasu lokalnego wiedząc, że czas ten zmienia się o 4 minuty na każdy stopień długości geograficznej:
61° * 4 min. = 244 min.
Zamieniamy minuty na godziny:
244 min. : 60 = 4 godz. 4 min.
Ponieważ Kraków leży na zachód od Madrasu uzyskaną różnicę czasu odejmujemy od czasu w Madrasie:
1600 - 4 godz. 4 min. = 1156
Odpowiedź:
W Krakowie jest godzina 1156 czasu słonecznego miejscowego.

Zadanie 2.
Która godzina czasu słonecznego miejscowego jest w Krakowie (20°E), jeżeli w Meksyku(99°W) jest godzina 1800 tego czasu?
Rozwiązanie:
Obliczamy różnicę długości geograficznej między Meksykiem a Krakowem:
99°W + 20°E = 119°
Obliczamy różnicę czasu lokalnego wiedząc, że czas ten zmienia się o 4 minuty na każdy stopień długości geograficznej:
119° * 4 min. = 476 min.
Zamieniamy minuty na godziny:
476 min. : 60 = 7 godz. 56 min.
Ponieważ Kraków leży na wschód od Meksyku uzyskaną różnicę czasu dodajemy do czasu słonecznego Meksyku:
1800 + 7 godz. 56 min. = 156
Odpowiedź:
W Krakowie jest godzina 156 czasu słonecznego miejscowego (w dniu następnym).

Zadanie 3.
Oblicz długość geograficzną miejsca, w którym Słońce góruje o godzinie 1524 czasu uniwersalnego?
Rozwiązanie:
Czas uniwersalny jest to czas słoneczny miejscowy południka 0°, więc na tym południku jest godzina 1524 czasu lokalnego. Natomiast na szukanym południku Słońce góruje, więc jest godzina 1200 czasu lokalnego. Możemy zatem obliczyć różnicę czasu między tymi południkami:
1524 - 1200 = 3 godz. 24 min. = 204 min.
Wiemy, że na każdy stopień długości geograficznej czas lokalny zmienia sie o 4 minuty, więc możemy obliczyć różnicę w długości geograficznej między danymi południkami:
204 min. : 4 = 51°
Szukany południk ma czas mniejszy od czasu uniwersalnego, więc znajduje się o 51° na zachód od południka 0°. Zatem jego długość geograficzna wynosi 51°W.
Odpowiedź:
Miejsce gdzie Słońce góruje o godzinie 1524 czasu uniwersalnego położone jest na południku 51°W.

Zadanie 4.
Oblicz długość geograficzną miejsca, gdzie 4 lipca Słońce góruje w momencie, gdy Polskie Radio podało, że jest godzina 830?
Rozwiązanie:
Na poszukiwanym południku Słońce góruje, więc jest godzina 1200 czasu słonecznego miejscowego. Natomiast godzina 830 jest na południku 30°E, gdyż w dniu 4 lipca w Polsce obowiązuje czas letni. Jesteśmy wtedy w strefie czasu wschodnioeuropejskiego. A czas ten jest określany według czasu słonecznego miejscowego południka 30°E. Po przeprowadzeniu tego rozumowania możemy przystąpić do obliczeń:
Obliczamy różnicę czasu:
1200 - 830 = 3 godziny 30 minut = 210 minut
Wiemy, że na każdy stopień długości geograficznej czas lokalny zmienia sie o 4 minuty, więc możemy obliczyć różnicę w długości geograficznej między danymi południkami:
210 min. : 4 = 52,5°
Szukany południk ma czas większy od czasu południka 30°E, więc leży o 52,5° na wschód od tego południka.
Obliczamy długość geograficzną szukanego południka:
30°E + 52,5° = 82,5°E
Odpowiedź:
Długość geograficzna poszukiwanego miejsca wynosi 82,5°E.

Zadanie 5.
Samolot z Londynu do Sydney (34°S 151°E) wystartował 10 maja o godzinie 1600 czasu uniwersalnego. Podaj datę i godzinę (według czasu strefowego Sydney) lądowania samolotu, jeżeli podróż trwa 13 godzin?
Rozwiązanie:
W pierwszej kolejności należy określić jaka jest różnica czasu strefowego Londynu i Sydney. Można skorzystać z mapy "Strefy czasowe", z której odczytujemy, że Sydney leży w strefie UT+10h (to znaczy, że czas w Sydney jest o 10 godzin większy od czasu uniwersalnego).
Jeżeli nie dysponujemy mapą można określić strefę czasową Sydney rysując na kartce papieru kolejne strefy czasowe (najłatwiej zaznaczając tylko południki środkowe) zaczynając od czasu uniwersalnego, a kończąc na czasie Sydney(będzie to ta strefa, której południk środkowy leży najbliżej Sydney):

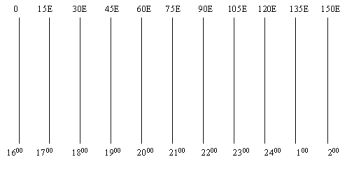
rys1. Schematyczny rysunek południków środkowych kolejnych stref czasowych.
Każda z tych metod doprowadza nas do wniosku, że Sydney ma czas o 10 godzin większy od Londynu. Zatem gdy samolot startuje 10 maja o godzinie 1600 z Londynu, to w Sydney jest 10 godzin później - 200 11 maja. Ponieważ samolot leci 13 godzin, to w Sydney wyląduje też 13 godzin później - będzie tam godzina 1500 11 maja.
Odpowiedź:
Samolot wyląduje w Sydney 11 maja o godzinie 1500.

Zadanie 6.

Oblicz, o której godzinie czasu urzędowego Słońce góruje nad Ciechanowem (52º52`N 20º35`E) w dniu 5 stycznia.

Rozwiązanie:
5 stycznia obowiązuje w Polsce czas urzędowy zimowy, czyli czas słoneczny południka 15ºE. 
Obliczamy różnicę w długości geograficznej między południkami:  20º35`E-15ºE=5º35`
Obliczamy różnicę czasu między tymi południkami: 5º*4min/1º=20min  35`*4s/1`=140s = 2min 20s co daje łącznie 22min 20s
Południk 15E leży na zachód od Ciechanowa, więc czas na nim jest mniejszy 12.00 -22min 20s = 11.37.40

Odpowiedź:
5 stycznia Słońce góruje nad Ciechanowem

GRUPA MEDIA INFORMACYJNE & ADAM NAWARA