 Ruch jednostajny prostoliniowy Ruch jednostajny prostoliniowy
Ruch jednostajny prostoliniowy jest ruchem, w którym ciało
porusza się ze stałą prędkością (v), czyli ciało pokonuje taką samą
drogę (przemieszczenie – s) w każdej jednostce czasu (np. w 1 s). Aby
można było mówić o ruchu jednostajnym na ciało nie może działać żadna
siła lub siły, które na nie działają muszą się wzajemnie równoważyć (w
tym ruchu spełniona jest I zasada dynamiki Newtona). Prędkość ciała
możemy wyliczyć ze wzoru v=s/t, gdzie t to czas trwania ruchu. Prędkość
jest wielkością wektorową, kierunek i zwrot jej wektora jest zawsze taki
sam jak przemieszczenia (s). Odległość od wybranego układu odniesienia
obliczymy wzorem (jest to równanie ruchu jednostajnego): x0=x1+vt, gdzie x0 – początek układu odniesienia, x1 – odległość od początku układu, miejsce z którego wyruszono. Przyjrzyjmy się teraz wykresom dla ruchu jednostajnego.
Wykres prędkości od czasu ruchu jest linią prostą równoległą do osi
OX, a drogę jaką pokonuje ciało możemy obliczyć jako pole figury pod
wykresem, podobnie jest w innych ruchach np. jednostajnie
przyspieszonym.
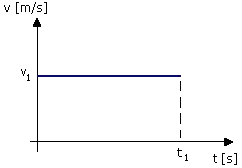
Wykres zależności prędkości od czasu – v(t)
Na wykresie drogi od czasu widać, że ciało pokonuje taką samą drogę (s), co sekundę.
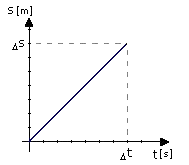
Wykres zależności drogi od czasu -s(t)
 Ruch jednostajnie przyspieszony prostoliniowy Ruch jednostajnie przyspieszony prostoliniowy
Ruch jednostajnie przyspieszony prostoliniowy jest ruchem, w
którym prędkość ciała wzrasta o stałą wartość (jednostajnie) co
jednostkę czasu (np. co sekundę) – jest to przyspieszenie, oznaczamy je
literą a i możemy wyliczyć je ze wzoru a=Dv/t, gdzie Dv
to zmiana prędkości, a t – czas, w którym ta prędkość uległa zmianie.
Podobnie jak prędkość tak i przyspieszenie jest wielkością wektorową,
jednak jego zwrot jest zawsze zgodny ze zwrotem działającej na ciało
siły wypadkowej. Jednostką przyspieszenia jest m/s2. Aby mógł się odbywać ruch jednostajnie przyspieszony na ciało musi działać niezrównoważona siła Fw (jedna lub kilka, których wypadkowe są różne od zera), przy czym
przyspieszenie jakie osiąga ciało jest wprost proporcjonalne do siły
wypadkowej i odwrotnie proporcjonalne do masy ciała; a=Fw/m (jest to treścią II zasady dynamiki Newtona).
Do wyprowadzenia wzoru na drogę jaką ciało pokonało poruszając się
ruchem jednostajnie przyspieszonym posłużymy się wykresem prędkości od
czasu (wyk. 1) – założymy ze prędkość na początku ruchu jest równa zero
(czyli ciało rusza z miejsca z przyspieszeniem a). Jak już wspomniałem w
pracy o ruchu jednostajnym drogę możemy obliczyć jak pole figury pod
krzywą prędkości na wykresie v(t), w tym wypadku jest to trójkąt, więc:
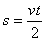 , przekształcając wzór na przyspieszenie otrzymujemy v=at, co po podstawieniu daje nam końcową formę tego wzoru: , przekształcając wzór na przyspieszenie otrzymujemy v=at, co po podstawieniu daje nam końcową formę tego wzoru:
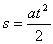
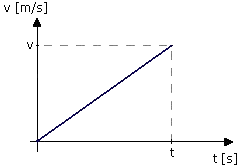
Wyk. 1. Wykres zależności prędkości od czasu – v(t) w ruchu jednostajnie przyspieszonym bez prędkości początkowej
Jednak co by było gdyby ciało poruszało się już z jakąś prędkością (v0 – prędkość początkowa) i przyspieszyło do prędkości końcowej (vk)?
Wzór na przyspieszenie pozostałby bez zmian, jednak wcześniej
wyprowadzony wzór na drogę byłby bezużyteczny. Przyjrzyjmy się zatem
wykresowi 2, figura pod prostą składa się z prostokąta, którego boki
tworzą prędkość v0 i czas t oraz trójkąta o podstawie t i wysokości vk-v0 (Dv), zatem:
s=v0t+Dvt/2, Dv=at, więc:
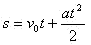
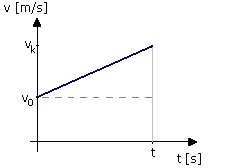
Wyk. 2. Wykres zależności prędkości od czasu – v(t) w ruchu jednostajnie przyspieszonym z prędkością początkową
Łatwo zauważyć, że taka forma wzoru jest uniwersalna, bo gdy nie ma prędkości początkowej wzór przyjmuje prawidłową formę s=at2/2. Równanie ruchu przedstawia się następująco:
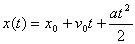
, gdzie:
x(t) – odległość przebyta od początku układu odniesienia
x0 – odległość miejsca rozpoczęcia ruchu od początku układu odniesienia
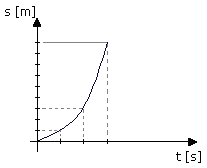
Wyk. 3. Wykres zależności drogi od czasu – s(t) w ruchu jednostajnie przyspieszonym
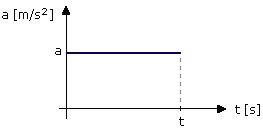
Wyk. 4. Wykres zależności przyspieszenia od czasu – a(t) w ruchu jednostajnie przyspieszonym.
 Ruch jednostajnie opóźniony prostoliniowy Ruch jednostajnie opóźniony prostoliniowy
Przed przeczytaniem tej pracy polecam zapoznać się z pracą o
ruchu jednostajnie przyspieszonym. Podobnie jak w ruchu jednostajnie
przyspieszonym w ruchu jednostajnie opóźnionym występuje a – opóźnienie,
mówi ono o jaką wartość prędkości na jednostkę czasu zmniejszy się
prędkość ciała. W tym ruchu przyśpieszenie ma wektor przeciwny do
wektora prędkości, ale zgodny z kierunkiem i zwrotem wektora siły
wypadkowej. W tym ruchu spełniona jest II zasada dynamiki Newtona.
Opóźnienie możemy obliczyć wzorem a=Dv/t.
Dysponując wiedzą, że drogę jaką pokonuje ciało możemy wyliczyć jako
pole figury znajdującej się pod prostą na wykresie prędkości od czasu
v(t) możemy przystąpić do wyprowadzenia wzorów na drogę (s). W
przypadku, gdy ciało porusza się z prędkością początkową v0,zwalnia z opóźnieniem i zatrzymuje się z prędkością końcową równa zero (vk=0),
figura powstała pod prostą jest trójkątem (wyk. 1), którego podstawą
jest czas trwania ruchu – t, a wysokością zmiana prędkości (Dv=v0-vk), więc:
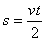 , a skoro v=at to podstawiając do wzoru: , a skoro v=at to podstawiając do wzoru:
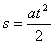 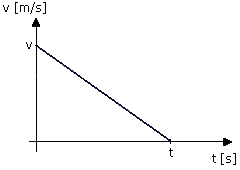
Wyk. 1. Wykres zależności prędkości od czasu – v(t) w ruchu jednostajnie opóźnionym, w którym prędkość końcowa jest równa zero.
Tak samo wyznaczymy wzór na drogę w przypadku gdy prędkość końcowa
ciała jest różna od zera (wyk. 1). Pole figury pod prostą to prostokąt o
boku v0 i t, odjąć trójkąt o podstawie t i wysokości Dv. Tak więc:
s=v0t-Dvt/2, gdzieDv=at, dlatego:
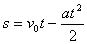
Równanie ruchu przedstawia sięnastępująco:
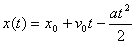
, gdzie:
x(t) – odległość przebyta od początku układu odniesienia
x0 – odległość miejsca rozpoczęcia ruchu od początku układu odniesienia
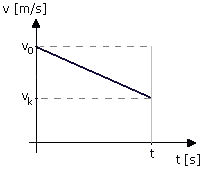
Wyk. 2. Wykres zależności prędkości od czasu – v(t) w ruchu jednostajnie opóźnionym, w którym prędkość końcowa nie jest równa zero.
GRUPA MEDIA INFORMACYJNE & ADAM NAWARA |