 Momenty bezwładności Momenty bezwładności
Twierdzenie Steinera: I = I0+md2
Jeżeli moment bezwładności ciała o masie m względem osi przechodzącej przez jego środek masy wynosi I0, to kiedy przesuniemy ją równolegle na odległość d moment bezwładności zwiększymy o wielkość md2
Punkt materialny w odległości R od osi obrotu
I = mR2

Pręt o długości L – oś obrotu prostopadła do pręta, przechodząca przez jego środek
I = 1/12 mL2
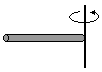
Pręt o długości L – oś obrotu prostopadła do pręta, przechodząca przez jego koniec
I = 1/3 mL2

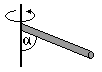
Pręt o długości L odchylony od pionu o kąt α – oś obrotu prostopadła do pręta, przechodząca przez jego koniecI = 1/3 mL2 sin2α
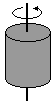
Walec o promieniu R – oś obrotu pokrywa się z osią walca
I = 0,5mR2
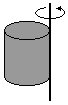
Walec o promieniu R – oś obrotu przechodzi przez krawędź walca
I = 1,5mR2
Walec o promieniu R i długości L – oś obrotu prostopadła do osi walca, przechodząca przez jego środekI = 1/12 m(L2+3R2)
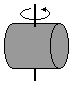
Walec wydrążony o promieniu R i promieniu wydrążenia r
I = 1/2 m(R2+r2)
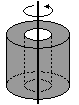
Pierścień o promieniu R (także cylinder i obręcz)
I = mR2
Wzór tym bardziej poprawny im ściany cylindra/pierścienia/obręczy są cieńsze
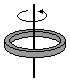
Pierścieńo promieniu R (także cylinder i obręcz) – oś obrotu przechodzi przez krawędź
I = 2mR2
Wzór tym bardziej poprawny im ściany cylindra/pierścienia są cieńsze
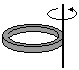
Krążek o promieniu R – oś obrotu pokrywa się z jego osią
I = 0,5mR2
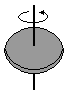
Krążek o promieniu R
I = 0,25mR2
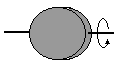
Sfera o promieniu R (cienkościenna powierzchnia kuli) – oś wzdłuż średnicy
I = 2/3 mR2
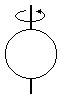
Kula o promieniu R – oś obrotu przechodzi przez środek kuli
I = 0,4mR2
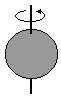
Kula o promieniu R – oś obrotu styczna do powierzchni kuli
I = 1,4mR2

Elipsoida o prostopadłych do osi obrotu osiach a i b
I = 0,2m(a2+b2)

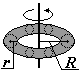
Torus o promieniach R i r
I = m(R2+0,75r2)
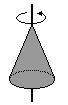
Stożek o promieniu podstawy RI = 0,3mR2
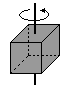
Sześcian o krawędzi a
I = 1/6 ma2
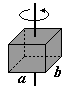
Prostopadłościan o krawędziach podstawy a i b
I = 1/12 m(a2+b2)
GRUPA MEDIA INFORMACYJNE & ADAM NAWARA |