 Jak liczyli Babilończycy Jak liczyli Babilończycy
Matematyka obszaru starożytnej Mezopotamii jest zazwyczaj nazywana babilońską, ze względu na to, że najliczniejsze źródła (około 400 glinianych tabliczek) pochodzą z wykopalisk babilońskich. Tabliczki te były zapisywane wówczas, gdy glina była jeszcze miękka, po czym były wypalane w piecu lub na słońcu.
Większość wykopanych tabliczek jest datowana na okres 1800–1600 p.n.e. i dotyczy między innymi takich zagadnień, jak ułamki, równania kwadratowe i sześcienne oraz znajdowanie trójek liczb naturalnych, spełniających twierdzenie Pitagorasa. Jedna z tabliczek podaje przybliżenie liczby z dokładnością do pięciu miejsc po przecinku.
Babilończycy używali systemu liczbowego o podstawie 60 (system sześćdziesiątkowy). Podział okręgu na 360 (= 6 × 60) stopni, a w konsekwencji podział godziny na 60 minut i minuty na 60 sekund, wywodzi się właśnie z matematyki babilońskiej. Trudno odpowiedzieć na pytanie, dlaczego Babilończycy obrali za podstawę akurat 60. Być może jest to związane z przybliżoną liczbą dni w roku (6 × 60 = 360), lecz nie jest to pewne. Pozycyjność systemu liczbowego oznacza, że zapis liczb był prowadzony w kilku kolumnach, zaś każda zawierała jako mnożnik kolejne potęgi liczby 60, np. 374 = 6 × 601 + 14 × 600 = 360 + 14 (współczesny zapis matematyczny jest analogiczny, lecz jego podstawą jest 10). Cyfry od 1 do 9 wyglądały następująco:
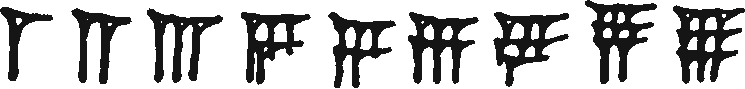
zaś cyfry 10, 20, 30, 40 i 50 wyglądały tak:

Brakujące cyfry pomiędzy 10 a 59 otrzymywano przez kombinację powyższych. Na przykład 11 otrzymywano przez połączenie dziesiątki z jedynką:

Natomiast liczby większe od 59 były otrzymywane przez układanie cyfr w kolejnych kolumnach. Przykładowo, liczba 70 = 1 × 60 + 10 była zapisywana jako

Na słynnej glinianej tabliczce nazwanej Plimpton 322, pochodzącej z ok. 1800 p.n.e., czyli ponad tysiąc lat przed Pitagorasem, zapisane zostały obliczenia długości boków trójkątów prostokątnych, zgodnie z twierdzeniem Pitagorasa. Tabliczka ta jest zapisana z prawa na lewo. W pierwszej kolumnie są podane kolejne numery porządkowe, kolumna druga zawiera słowo „liczba”, zaś kolumna trzecia zaczyna się od słowa „długość”, po czym wymienione są kolejne wartości a. Kolumna czwarta zaczyna się od słowa „przekątna”, po czym zapisane są kolejne wartości c. Ostatnia kolumna zawiera wartości b, obliczone zgodnie ze wzorem b2 = c2 – a2, z dokładnością co najmniej do czwartego miejsca po przecinku.

W Mezopotamii nie znano zera ani jako liczby (którą można dodawać, mnożyć, itd.), ani jako cyfry. Wskutek tego ten sam napis mógł oznaczać zarówno 11, 601, 36001, jak i 36060. Dopiero za panowania Seleucydów (około roku 400 p.n.e.) na tabliczkach klinowych w zapisie liczb pojawia się symbol dwóch klinów, które oznaczają nieobecność cyfry w danej pozycji (…).
GRUPA MEDIA INFORMACYJNE & ADAM NAWARA |