 Jak sobie radzili mierniczy z Egiptu? Jak sobie radzili mierniczy z Egiptu?
Doroczne wylewy Nilu, będące błogosławieństwem Egiptu oraz podstawą egzystencji i dobrobytu Egipcjan, niszczyły granice uprawnych poletek, więc corocznie trzeba było je odtwarzać, aby po ustąpieniu wody fellachowie mogli zabrać się do roboty. Wówczas cała armia urzędników-mierniczych wyruszała w teren, by sprostać temu zadaniu. Oczywiście, nie wypatrywano zeszłorocznych granic, bo te przykryła gruba warstwa mułu, ale mniej więcej w tym samym miejscu wyznaczano nowe, by – zgodnie z rejestrem – nowe poletko miało taki sam areał, co w zeszłym roku. Poletka nad Nilem miały różne kształty – najczęściej były to czworoboki, czasem trapezy, rzadziej prostokąty (bo ukształtowanie terenu rzadko na to pozwalało), a niekiedy były trójkątne.
Egipcjanie zdawali sobie sprawę z tego, że wielkość pola powierzchni poletka zależy od jego długości i wielkości jego „podstawy”, czyli długości boku „na oko” najbardziej prostopadłego do wcześniej zmierzonego, a że sąsiadujące ze sobą boki poletek na ogół były dalekie od prostopadłości, obliczenia pola dokonywali w sposób odmienny od stosowanego przez nas dzisiaj, acz do niego zbliżony, dla ówczesnych mierniczych technicznie prosty, nie wymagający żadnych innych przyrządów pomiarowych oprócz „kraczki1”, podstawowego dla nich instrumentu. Mierzyli bowiem długości wszystkich czterech boków czworokąta, nazwijmy je kolejno a, b, c, d, następnie tworzyli średnie boków przeciwległych i mnożyli przez siebie. Otrzymana w ten sposób liczba S była przybliżeniem miary pola. Napis na ścianie świątyni Horusa w Edfu opisuje m.in. podarowane poletka, wymieniając długości ich boków i podając wielkość ich pól, z czego wynika, że pola czworobocznych poletek obliczano wg powyższego schematu:
(1) (a+c)/2 x (b+d)/2 = S
Pewna liczba poletek wymienionych w tym napisie miała kształt trójkątny, który opisywano mnie więcej wg następującego schematu: zachodnią stroną jest a, wschodnią jest c, południową jest b, północną jest „nic”; pole takiego poletka podawano jako:
(2) (a+c)/2 x b/2 = S
W praktyce staroegipskich rachmistrzów obliczanie pól wcale nie przebiegało tak gładko, jak podają powyższe schematy. Oto, np., problem 52 w papirusie Rhinda (R 52 – [1], s. 93):
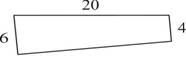
Przykład zrobienia obciętego trójkąta ziemi. Jeżeli powiedziano Tobie: obcięty trójkąt ziemi z 20 khet na jego boku i 6 khet w jego podstawie oraz 4 khet na (linii) obcięcia. Co jest jego polem? Dodaj podstawę do obcięcia, otrzymasz 10. Weź 1/2 z 10, mianowicie 5 dla dania mu (kształtu) prostokąta. Wykonaj mnożenie: 20 razy 5, otrzymasz 100. Pole jego takie jest. Czynności takie spotykasz:
1 1000 \1 2000
1/2 500 2 4000
\4 8000
Całość 10000
Jego polem jest 100 setat (10 10-setat)
Technika obliczeń nie wymaga komentarza, bo przebiegają one zgodnie z wzorem (1), natomiast objaśnić trzeba występujące tu jednostki miar. Podana w zadaniu miara długości khet zawiera 100 łokci, a setat jest miarą pola równą kwadratowi o boku długości 10 łokci, czyli 1 setat = (10 łokci)2 = 100 kwadratowych łokci, czasem nazywany łokciową wstęgą, zwłaszcza gdy poletko miało kształt prostokąta o długości 1 kheta i szerokości 1 łokcia; większą jednostką pola był 10-setat (...)
GRUPA MEDIA INFORMACYJNE & ADAM NAWARA |