 Geometria i sztuka Geometria i sztuka
Kiedy jako uczniowie szkoły podstawowej, lub średniej, słuchamy na lekcjach matematyki o antycznych matematykach i ich osiągnięciach, to przyjmujemy wszystko w sposób dosłowny. Skoro nauczyciel mówi nam o twierdzeniu Pitagorasa, to wyobrażamy sobie, że kiedyś, ktoś o tym nazwisku napisał i udowodnił wzór a2 + b2 = c2, gdzie a, b i c są długościami boków trójkąta prostokątnego.
Nawet przez chwilę nie nachodzą nas wątpliwości, czy aby Pitagoras umiał napisać taki wzór, czy on rzeczywiście wymyślił takie twierdzenie, itd. Nikt się nie zastanawia, skąd my czerpiemy wiedzę o Pitagorasie i wielu innych matematykach z przeszłości. Pewnie wydawano w tamtych czasach jakieś książki i sprzedawano je w tamtejszych księgarniach? Pewnie egzemplarz takiej książki dotarł do naszych czasów i stąd my wiemy o Pitagorasie i wielu innych?
Jak to jest naprawdę z naszą wiedzą o matematyce i matematykach z przeszłości? Co my wiemy na pewno, a czego się tylko domyślamy? Wróćmy zatem do dalekiej przeszłości i zastanówmy się przez chwilę nad tym wszystkim.
Na początek proponuję, abyśmy cofnęli się w czasie o 5500 lat i zajrzeli do Mezopotamii. Tu, w dolinie rzek Tygrysu i Eufratu, na obszarze obecnego Iraku, istniały kolejno trzy wielkie i ważne cywilizacje. Pierwszą z nich byli Sumerowie (4300 p.n.e. do 2000 p.n.e.), drugą nakładającą się na okres sumeryjski byli Akadyjczycy (2300 p.n.e. do 2100 p.n.e.) i wreszcie trzecią cywilizacją byli Babilończycy (2000 p.n.e. do 540 p.n.e.). Historia Mezopotamii jest niezwykle interesująca, ale nas będzie interesowała matematyka z tej części świata i to, jak do nas dotarła.
Sumeryjczycy rozwinęli rodzaj pisma zwany klinowym. Były to odciśnięte w surowej glinie znaki w kształcie klina. Tabliczki z takimi tekstami były następnie suszone na słońcu i używane w podobny sposób, w jaki my używamy obecnie notatki na papierze. Kolekcje tabliczek tworzyły coś w rodzaju archiwów i książek. Taka „książka” mogła mieć dość dużą wagę i była kłopotliwym obiektem do przechowywania, ale o dziwo, duże kolekcje tabliczek z pismem klinowym zachowały się w suchym i gorącym klimacie tej części świata. Archeologowie i uczeni odkryli i zbadali ogromną liczbę takich tabliczek. Wiele z nich to tabliczki z elementami matematyki. Są tu tablice mnożenia liczb, zbiory prostych problemów matematycznych, wykazy płac robotników, tablice meteorologiczne, tablice z tzw. praktyczną matematyką, itd.
Zanim pokażemy dwa przykłady takich tabliczek z matematyką zapisaną pismem klinowym, warto zastanowić się przez chwilę nad tym, jak można coś takiego przetłumaczyć na języki współczesne. Na początek zauważmy, że dokładne tłumaczenie dowolnego języka współczesnego na inny język współczesny może być poważnym problemem i nie zawsze jest wykonalne. Jeszcze trudniej było przetłumaczyć teksty pisane w językach sumeryjskim, akadyjskim i wielu innych na współczesny angielski. Dodatkowo zniszczenia, najczęściej brzegów tabliczek, powodują, że tłumaczenie takowe jest bardziej zgadywaniem sensu niż wiernym tłumaczeniem. Tak właśnie jest z paroma tekstami matematycznymi z Mezopotamii. Na początek przyjrzyjmy się jednej z najsłynniejszych tabliczek z pismem klinowym i matematyką.
Pokazana na ilustracji (fig. 1) tabliczka z pismem klinowym nosi nazwę Plimpton 322 od nazwiska George A. Plimptona nowojorskiego wydawcy, właściciela kolekcji glinianych tabliczek z pismem klinowym z obszaru Mezopotamii, przechowywanej obecnie w Columbia University. Interesujące jest to, że przez wiele lat różni naukowcy toczyli dyskusję nad sensem kolumn znaków umieszczonych na tabliczce. Początkowo uważano, że jest to spis operacji handlowych. Dopiero Otto Neugebauer zwrócił uwagę na to, że liczby na tabliczce mają związek z tzw. trójkami pitagorejskimi. W książce The Book of Numbers (patrz [3]) autorzy pokazują, że ta ostatnia koncepcja jest najbardziej prawdopodobna. To zaś oznacza, że Babilończycy, a być może nawet wcześniej Sumerowie, znali pewną formę tego, co my obecnie nazywamy twierdzeniem Pitagorasa. Z pewnością nie był to wzór, jaki my znamy obecnie. W literaturze możemy odszukać tłumaczone fragmenty tabliczek nawiązujące do twierdzenia Pitagorasa. Oto jedno z nich pochodzące z British Museum 9…)

Fig. 1. Tabliczka z pismem klinowym, określana jako Plimpton 322, pochodząca z okresu 1970 p.n.e. do 1700 p.n.e. (komputerowo poprawiona wersja zdjęcia z Wikimedia Commons, MLM)
o 4 jest długością, a 5 jest przekątną [prostokąta]. Jaka jest szerokość?
o Jej wartość jest nieznana.
o 4 razy 4 jest 16.
o 5 razy 5 jest 25.
o Jeśli odejmiesz 16 od 25, to otrzymasz resztę 9.
o Jaką liczbę powinienem pomnożyć przez siebie, aby otrzymać wynik 9?
o 3 razy 3 jest 9.
o 3 jest szerokością.
Jak łatwo można zauważyć, podany tu przykład jest prostym algorytmem obliczania długości jednego z boków trójkąta prostokątnego. Podobne podejście możemy znaleźć w wielu innych kulturach starożytnych. Słynna chińska księga pisana przez kilka generacji matematyków od 10 p.n.e. do 2 wieku p.n.e. – Jiuzhang Suanshu, znana na Zachodzie jako Dziewięć rozdziałów o sztuce matematycznej, jest również zbiorem podobnych do tego algorytmów.
Asger Aaboe w swojej książce Episodes from the early history of mathematics pisze, że znaleziono i zbadano około 400 tabliczek z tekstami matematycznymi. W okresie przed wojną w Iraku liczba ta znacznie się zwiększyła i nasza wiedza o matematyce babilońskiej jest już znacznie bardziej kompletna. Zauważmy przy okazji, że choć dużo wiemy o matematyce babilońskiej, to absolutnie nic nie wiemy na temat tych, co ją tworzyli. Na glinianych tabliczkach nie ma bowiem nazwisk autorów.
Przez moment popatrzmy na jeszcze jeden przykład matematyczny z Mezopotamii. Tym razem jest to gliniana tabliczka YBC 7289 z kolekcji Yale University (pochodząca z okresu 1900 p.n.e do 1700 p.n.e.), pokazująca, jak obliczyć przekątną kwadratu (fig. 2).

Fig. 2. Tabliczka z pismem klinowym (YBC 7289, 1900 p.n.e. – 1700 p.n.e.) pokazująca przybliżoną wartość (fotografia pochodzi z kolekcji Jeremiego Normana (patrz [5]), użyta za pozwoleniem autora).
Ciąg znaków pisma klinowego na przekątnej kwadratu oznacza ciąg liczb 1, 24, 51, 10. W systemie sześćdziesiątkowym oznacza on liczbę
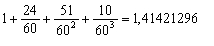
Jak widać z powyższego przykładu, Babilończycy umieli zdumiewająco dokładnie wyliczyć pierwiastek kwadratowy z liczby 2 i z całą pewnością nie jest to wynik mierzenia przekątnych, ani małych, ani nawet bardzo dużych kwadratów (…)
GRUPA MEDIA INFORMACYJNE & ADAM NAWARA |